Before writing this article, I took time to explain the concept of memoization to my mom, whose background is in nursing just so I could see what extra knowledge a beginner on this concept would need to better understand the concept of memoization. So, thank you to my amazing mom for unknowingly being a 'guinea pig' to this article😅. Enough of the stories, let's dive in...

What is memoization?

Memoization is a technique used to optimize your code that stores computations in cache memory. This is temporary data storage that makes data retrieval easier and faster and retrieving that same information from the cache memory instead of computing it again.

Algorithm question to understand memoization:

To better understand the concept of memoization, let's go through an example of an algorithm that applies this same concept. We will go through the problem of finding the Fibonacci of an integer n. The Fibonacci of an integer n is computed using the formula below: Fibonacci(n)= Fibonacci(n-1) +Fibonacci(n-2)

For example: 5) = Fibonacci (4) +Fibonacci (3)

Fibonacci (100) = Fibonacci (99) +Fibonacci (98)

Your first thought on solving this problem was probably to use recursion. And that is a great idea and would be efficient for a small value of n. However, as the value of n gets bigger, the recursion function becomes very inefficient. Below is an illustration of how the recursive function will work

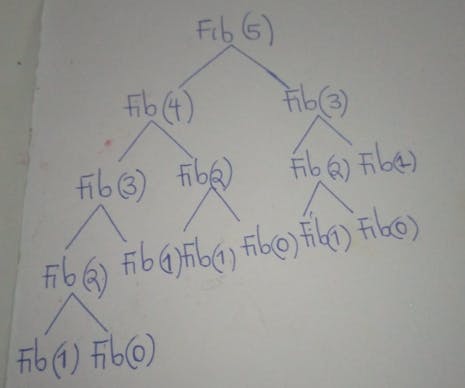
Now imagine that same action for an integer as big as 100.

Say, however, that once we computed the Fibonacci of an integer n, we stored it in memory such that when finding the Fibonacci of an integer larger than it, we would not have to start from scratch. For example, say we wanted to find the Fibonacci of 7 but we had already computed the Fibonacci of 5, all we'd have to do is retrieve the already computed result of the Fibonacci of five and add that result to 6 and voila! we have our solution; Way easier than using the top-down approach to find the Fibonacci of 7 from scratch right?

Below is a code snippet of three ways I solved the problem of finding the Fibonacci for an integer n, together with space and time complexity analysis of each method used.

Method 1: Recursion

    def fib(self, n):
        """
        :type n: int
        :rtype: int
        """
        if n==0:
            return 0
        if n==1:
            return 1
        return self.fib(n-1)+ self.fib(n-2)

#The time complexity for the recursive function is O(2^n) as the approximate number of states required to compute the Fibonacci of n is 2^n. 
#Refer to the illustration above for a better understanding. 
#The space complexity on the other hand will depend on the depth 'n' of the tree formed when computing the Fibonacci of an integer n, and if each function call takes 'm' memory, then the space complexity will be O(mn)

Method 2: Memoization

      memo={}
        if n in memo:
            return memo[n]
        if n==0:
            memo[0]=0
            return 0
        if n==1:
            memo[1]=1
            return 1
        if n>1:
            memo[n]= self.fib(n-1)+self.fib(n-2)
            return memo[n]

#Using memoization, the Fibonacci of each integer will be calculated only once and stored in memory, therefore the space complexity will be O(n). The time complexity will be O(n) since, again, the Fibonacci of an integer n is calculated only once.

## Method 3: Iteration

```python
def fib (self, n): 
""": 
type n: int :rtype: 
int """ prev1, prev2=0,1 output=0 
    if n==0: 
        return 0 
    if n==1: 
        return 1 
    for i in range(2,n+1): 
        output= prev1+prev2 prev1=prev2 prev2=output
        return output

#This method has an O(1) space complexity as we are not using any extra memory and an O(n) time complexity.

With this new understanding, here is the link to this question on [Leetcode] so you can try it yourself. All the best with that and see you on our next analysis of a different data structure!

Your tips/ pointers in the comment section will go a long way towards helping me get better in my technical writing craft. Thank you!